Marine Engineering Specialists -- Bentley Systems has acquired Ultramarine's MOSES Software [ Press Release ]
Seakeeping

Overview Of Seakeeping:

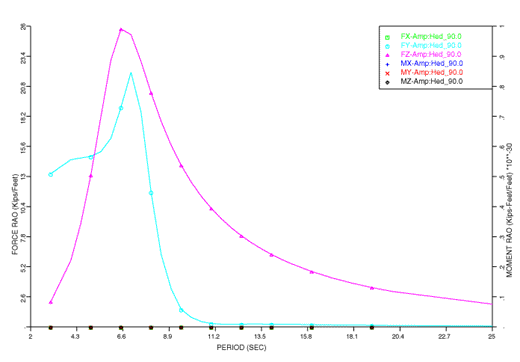
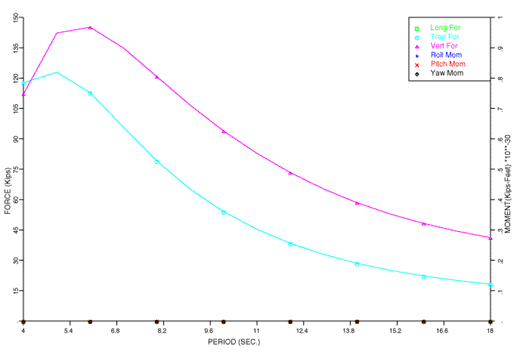
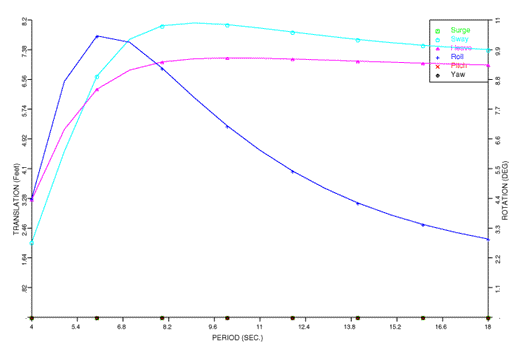
By seakeeping, we mean finding the motions and related quantities of a vessel subjected to a sea state. Normally, this is further restricted to mean that the motions are computed in the frequency domain. While we can compute the motions in other ways, here we will consider only the frequency domain. Now, in order to compute the motions, one must compute the forces. This is accomplished by using either Morison's' equation, two dimensional diffraction theory, or three dimensional diffraction theory. While the mathematics of these three theories differ, the important thing here is that they all compute the excitation force, the added mass, and the radiation damping for a vessel as a function of frequency and heading. When the equations of motions are solved for a unit amplitude wave, we obtain a set of quantities called Response Amplitude Operators, or RAOs. Here is a typical set of RAOs for a barge.

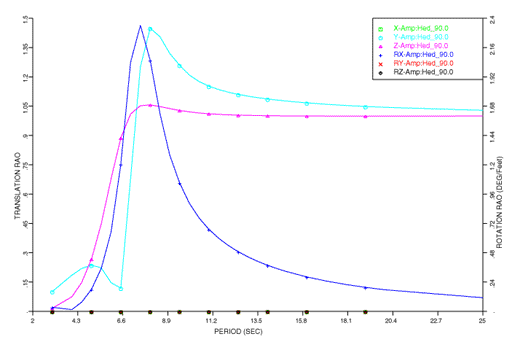
These results are for beam seas. Here, the curves of interest are heave, sway and roll. Of particular importance is that the heave is reasonably well behaved - increasing from zero at short periods to one in long periods, but the roll has a definite peak. Both the heave and the roll have "natural periods" within the period range plotted, but heave is "overdamped" by the radiation damping and roll is not. In fact, for roll we have added some viscous damping to obtain reasonable magnitudes. Without viscous damping the roll response would be far too large.

For semisubmersibles (and other similar vessels) the radiation damping is small for all degrees of freedom at the natural frequencies. Thus, for these shapes, viscous damping needs to be added in all degrees of freedom, not only roll. An RAO curve for a semi corresponding to the above is:

Notice that here there are quite a few more "bumps" in the curves. In fact, most have two distinct relative maxima. Where do these come from? First notice that (viewed simplistically) for each degree of freedom, we have a spring, mass and dashpot system, so we can expect large response at the natural frequency: 
        w = sqrt ( K/M )
The problem is that here M includes the added mass which depends on frequency. Thus, which M do we use to compute the natural frequency? Now, different people address this difficulty differently. We prefer to say that here there is no such thing as a natural frequency - only frequencies at which the response is larger than others. In addition to having M vary with frequency, the excitation force also varies. Thus, it is not surprising to get several relative maxima. The periods at which the maxima occur depend on the hull form (which defines the excitation, the added mass, and a part of the spring constant K) and the mass distribution (which determines the basic inertia and a contribution to K). For a given ship at a given draft and trim, we can change the RAOs quite a bit by moving mass around.

One important thing to remember is that since we added viscous damping, the problem became nonlinear. Now, the results can not, strictly speaking, be "scaled up" from unit amplitude to realistic values. What is "allowable" mathematically depends precisely on how we linearized the problem. There are two approaches one can use. First, one can use a constant steepness to linearize the system. Here the wave height used to compute the response is obtained from the frequency and the wave slope. The second approach is to spectrally linearize the system by computing the amplitude of a wave at each frequency that would follow from a specified spectrum. Both approaches seem to work fairly well and allow us to use the "RAOs" as if they were linear, provided they are used with spectra which are close to either the spectrum used to linearize the system, or have a mean steepness reasonably close to that used.

Now, the RAOs themselves are of limited use because we rarely encounter a "regular sea" (a sea composed of waves which look like sine waves). In reality, the sea is "confused" with peaks and valleys all over the place. Thus, a sea is normally specified by a spectrum - a function of frequency and heading which gives a measure of the square of the amplitude of a sine wave of this frequency and heading in the sea. With a spectrum and the RAOs, one can compute the "moments" of the response spectrum, but what does one do with moments of the response spectrum? Normally, one assumes a probability distribution (Raleigh is normally chosen) and uses it and the moments to compute probabilities of exceedence. The following:

shows the average of the 1000th highest peaks which occur in an 8 foot significant sea of various "periods". In comparing these curves with the previous ones, there is one obvious difference - the sharp peak in the roll curve is "broadened". In other words, the roll in real seas is not as sensitive to period as the response operator itself.

While the motions of the vessel are important, normally one is interested in not the motions themselves, but what they do to the cargo carried by the vessel. From the cargo's perspective moving the vessel does two things:

  • It produces an inertia load, and
  • It rotates the cargo frame of reference so that gravity appears to act in a different direction.
If we combine these two effects, we can plot a curve of the force induced on the cargo by the motions:

Now, let's compare the force RAOs with the motion ones. First, notice that the lateral force is produced by a combination of the sway acceleration at a point and the roll. The most striking thing about this comparison is that the peaks in the force occur at a lower period (higher frequency) than those for the motions. This is due to the fact that the force depends on the acceleration which is the frequency squared. If we look at statistics of the forces:

we find that again the statistics of the forces are not as sensitive to period as the RAOs themselves. Here, however, there is something more important to notice. The forces have a peak. Thus, if we have an estimate of the maximum wave that can occur at the period where the force peaks, we have an upper bound on the force itself. Now, we know that for a given wave period, there is a maximum wave because a wave will break before its height can exceed some height - length ratio.